arrow_back Back to Rich Tasks

Something in Common Rich Tasks

This page contains a truly wonderful set of activities created and kindly shared by John Burke. They allow consolidation of key skills, prevent students from copying each other (as all the questions are different), make marking and assessing easy for the teacher (as all the answers are the same!), and provide a lovely extra challenge for students as they try to figure out exactly what is going on! In short, I think they are amazing, and thank you so much to John for sharing them with us all.

Please note: the "Earliest Year Group" is just a guideline. I have often been able to use a "Year 8 Task" with my Year 11s, for example.

Contents

The Backgroundkeyboard_arrow_up

Back to Top

This set of resources came into being from my desire, as a teacher, to get pupils to think for themselves and not copy work from their neighbours.  I wish I could say that I did all the research and came up with this scheme but, in fact, it was serendipitous.  I put together a task for some sixth formers (SIC_6 "Annulus Volume of Revolution") where they all had different input parameters but all had the same answer, using a result I remembered from my sixth form days.  It went very well so I developed more resources for lower down the school.  As the pupils caught on there was the risk that they would just sit back and await the answer so one ruse I use is to give each worksheet a letter and say that I have a table of answers that I look up.  Then I introduced some activities where the answers are different but can easily be computed from the input parameters (if you know how) to avoid this issue.  A good example of this is SIC_11 "Triangle xy Area" where the teacher only has to multiply two integers together to know the answer but the pupils don't know that - yet.  I started off labelling my resources "Different Problem, Same Answer!" but that didn't really fit in the end so I ended up with "Something In Common".

Not all of the resources are mine.  Like all teachers I take inspiration from wherever I find it and so have included, for example, some RISPs by Jonny Griffiths and tasks from the nRich website and other places and I give due credit for a task where I remember where it came from.

Each resource has a suggested earliest year group.  This is solely for use by the Mathematics department at my school so that we can avoid the situation whereby a teacher has planned to use a resource and then find that some pupils say they have already completed the task in a previous year.  Please use a resource wherever you see fit.  Indeed, the earliest year group can be a bit misleading because although the scheme of work indicates that the knowledge to perform the task is imparted to that year group the maturity of their problem solving capabilities may not be up to it and so would need a lot of scaffolding anyway.  So, in a way, you can ignore the earliest year group information!  Just review the activity and use it where you see fit.

Because the worksheets are all different I have placed them in pdf format with 1-up, 2-up or 4-up printing already prepared.  All you need do is print the appropriate number of pages for the size of your class.  Every accompanying Powerpoint has a worked solution and the original worksheets can be found at the back of it (so you can create separate ones for visually impaired pupils, for example, or change wording).  Some activities have additional resources like Geogebra files for demonstration.  One even has a Scratch program!

I use the resources in different ways.  Sometimes I use them to introduce a topic (circle theorems and sine rule, for example), sometimes to consolidate the learning of a topic and sometimes to introduce a wow factor on a Friday.  But in every case I encourage/challenge them to find out how I did it and quite often they are up for the challenge, which I find very satisfying, and I hope they will tell their friends. 
I enjoy creating these resources and as of October 2016 there are 50 in the set.  They do take time but I and my colleagues at school reuse them a lot and I hope you will too.  As a result I would be grateful for any feedback, whether it is about mistakes or suggestions for improvement or indeed new ideas for a resource.

John Burke
(The Manchester Grammar School)
[email protected]

Earliest Year Group: Year 7keyboard_arrow_up

Back to Top

12. Quad Tessellate

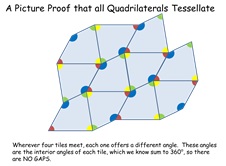
Get pupils to draw a quadrilateral that they think will not tessellate.  Then reproduce it using the Geogebra file and show that it does.  Then show a picture proof.

Worksheet	PowerPoint	Supporting Materials
None	Quad Tessellate Proof	Quad Tessellate (Geogebra) Quad Tessellate Animation (Geogebra)

15. Magic Fractions

nRich.  Using their own numbers (following a rule) the pupils form fractions and carry out operations on them.  All answers are the same.

Worksheet	PowerPoint	Supporting Materials
None	Magic Fractions	None

Earliest Year Group: Year 8keyboard_arrow_up

Back to Top

1. Think of a Number

Simple game that finishes on 1, whatever your starting number.  Leads to creating expressions and proof.

Worksheet	PowerPoint	Supporting Materials
None	Think of a Number	None

3. Parallelogram in Quadrilateral - Grid

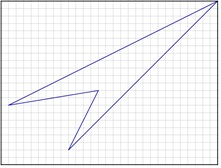
Bisect the sides of a quadrilateral to get a parallelogram.  All quadrilaterals are different but all parallelograms are identical.  The grid allows easy bisection.

Worksheet	PowerPoint	Supporting Materials
Parallelogram in Quadrilateral Grid	Parallelogram in Quadrilateral Grid	Parallelogram in Quadrilateral Animation (Geogebra)

31. Straight Line

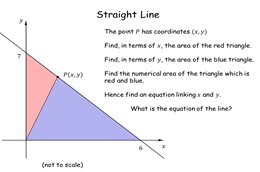
A very simple (but illuminating) task where pupils follow simple instructions and generate the equation of a straight line from consideration of areas of triangles.  Each equation is different but easy for the teacher to ascertain the answer by visual inspection.

Worksheet	PowerPoint	Supporting Materials
Straight Line	Straight Line	Straight Line (Geogebra)

39. Letter Wheel

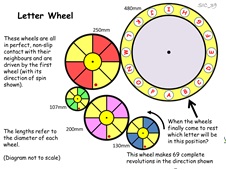
Pupils have to work out how much the last wheel of five connected wheels turns when told how much the first wheel turns.  Sixteen different answers but teacher knows each answer from information coded in the worksheet.  Can introduce modulo arithmetic.

Worksheet	PowerPoint	Supporting Materials
Letter Wheel	Letter Wheel	Letter Wheel (.sb2)

43. Pick a Polygon

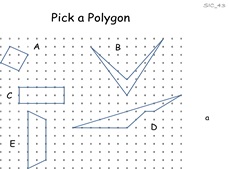
Pupils discover Pick's Theorem.  Each worksheet has different polygons but polygons allocated to a given letter have the same area.  They are invited to draw more polygons and discover the formula for the area.

Worksheet	PowerPoint	Supporting Materials
Pick a Polygon	Pick a Polygon	Proof of Pick

47. How Many Sides?

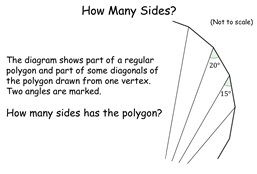
On the face of it this looks like a very tricky problem but in fact it is quite straightforward, only requiring knowledge of external angles and the sum of angles in a triangle!  Teacher can easily infer the answer and there is an interesting result at the end.

Worksheet	PowerPoint	Supporting Materials
How Many Sides?	How Many Sides?	None

Earliest Year Group: Year 9keyboard_arrow_up

Back to Top

4. Parallelogram in Quadrilateral - Compass

Bisect the sides of a quadrilateral to get a parallelogram.  All quadrilaterals are different but all parallelograms are identical.  A compass will be needed to bisect the sides.

Worksheet	PowerPoint	Supporting Materials
Parallelogram in Quadrilateral Compass	Parallelogram in Quadrilateral Compass	Parallelogram in Quadrilateral Compass Animation

7. Trapezium and Diagonals

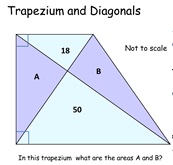
Work out the area of two triangles given the area of two others which all fit in a trapezium.  Each problem is different but all the answers are the same.

Worksheet	PowerPoint	Supporting Materials
Trapezium and Diagonals	Trapezium and Diagonals	None

35. Strange Guys

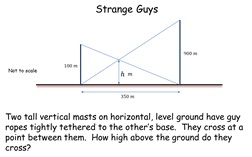
Classic problem involving masts and guy ropes solved using the application of similar triangles.  The activity brings out the fact that the distance between the masts is irrelevant to the question posed.  All the answers are the same (90 m). 

Worksheet	PowerPoint	Supporting Materials
Strange Guys	Strange Guys	None

41. Cross Bear!

Three bears start scoffing porridge at different rates and then start scoffing each other's.  Pupils have to work out the individual rates.  Teacher can find the answer encoded in the worksheet by multiplying a number by 10.

Worksheet	PowerPoint	Supporting Materials
Cross Bear!	Cross Bear!	None

42. The Obedient Ray

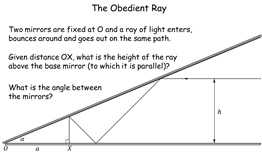
A light ray bounces between two mirrors and retraces its steps.  The angle (to be determined) between the mirrors is the same but the height of each ray is different.  Simple geometry yields the answer but pupils are invited to look at a more general case.

Worksheet	PowerPoint	Supporting Materials
The Obedient Ray	The Obedient Ray	None

45. Piscatorial Percentages

A counter-intuitive result involving percentages.  It's a nice little problem to solve algebraically but there is also a very simple way to do it which makes it even more worth doing.  I couldn't resist using some Escher artwork.

Worksheet	PowerPoint	Supporting Materials
Piscatorial Percentages	Piscatorial Percentages	None

Earliest Year Group: Year 10keyboard_arrow_up

Back to Top

16. Angle at Centre, Angle on Arc

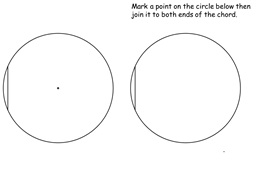
Discovery of two circle theorems.  Pupils mark out angles on a chord and cut them out and compare.

Worksheet	PowerPoint	Supporting Materials
Angle at Centre, Angle on Arc	Angle at Centre, Angle on Arc	Angle at Centre, Angle on Arc Resources Angle at Centre, Angle on Arc (Geogebra)

17. Multi-Simultaneous

Pupils are presented with a number of simultaneous equations to solve.  How quickly will they spot that they only need to select one pair?  How many will select the easiest pair rather than just the first two in the list?.......

Worksheet	PowerPoint	Supporting Materials
Multi Simultaneous	Multi Simultaneous	Multi Simultaneous (Excel)

18. Polygon in Annulus

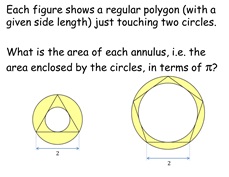
Pupils need to work out the area of a couple of rings with different dimensions - but the same area.

Worksheet	PowerPoint	Supporting Materials
Polygon in Annulus	Polygon in Annulus	Polygon in Annulus (Geogebra)

21. Leonardo of Pisa

Pupils are given the nth term of a sequence and are asked to find specific (non consecutive) terms in the sequence.  It is the Fibonacci sequence.  The task involves surds and indices.  Then they are asked to prove that the ratio of consecutive terms tends to the golden ratio.

Worksheet	PowerPoint	Supporting Materials
Leonardo of Pisa	Leonardo of Pisa	Leonardo of Pisa (Excel)

25. Crossed Lines

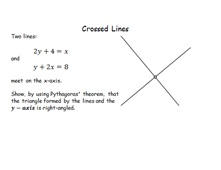
This tests the pupils' knowledge of straight line graphs and y=mx+c and the significance of gradients of perpendicular lines.

Worksheet	PowerPoint	Supporting Materials
Crossed Lines	Crossed Lines	Crossed Lines (Excel)

36. Quadthagoras!

Problem involving forming and solving a quadratic equation.  Not very hard and won't take long.  Can the pupils work out how all the answers are the same?

Worksheet	PowerPoint	Supporting Materials
Quadthagoras	Quadthagoras	None

44. Sea Shell Product

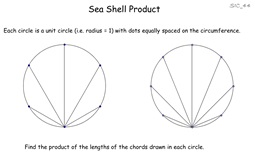
Pupils discover an intriguing result (that will be beyond them to prove) - the product of the lengths of the chords equals the number of equally spaced dots on the circle.  Quite simple trigonometry and lengths of sides of triangles.

Worksheet	PowerPoint	Supporting Materials
Sea Shell Product	Sea Shell Product	None

46. Squaring the Rectangle

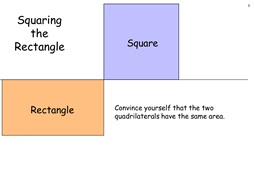
Pupils are asked to construct a square with area equal to a given rectangle, using construction methods only.  Gives practice in constructions and application of the intersecting chords theorem.  Leads to determining the square root of a number by construction.

Worksheet	PowerPoint	Supporting Materials
Squaring the Rectangle	Squaring the Rectangle	None

48. Three Circles and a Tangent

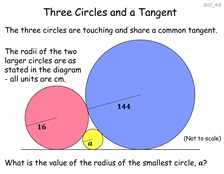
Pupils seem to be fazed when they first look at this problem, so it's worth doing.  It only requires Pythagoras' Theorem (like most Sangaku problems).  There is a neat answer to the general case.

Worksheet	PowerPoint	Supporting Materials
Three Circles and a Tangent	Three Circles and a Tangent	None

Earliest Year Group: Year 11keyboard_arrow_up

Back to Top

2. Sine Rule Discovery

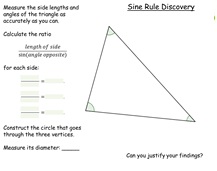
Measure the sides and angles and calculate the ratios.  All ratios in the class are the same, yet all of the triangles are different.

Worksheet	PowerPoint	Supporting Materials
Sine Rule Discovery	Sine Rule Discovery	None

8. Four Crescents

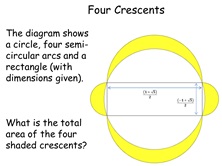
Four crescents are drawn around a rectangle.  All rectangles are different and the area of the crescents is equal to the rectangle.  Surd (area = 1) and non-surd (area = 900) versions available.

Worksheet	PowerPoint	Supporting Materials
Four Crescents	Four Crescents	Four Crescents 900 Four Crescents (Geogebra)

11. Triangle xy Area

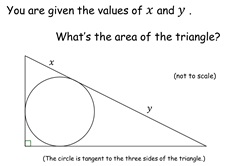
Work out the area of a triangle with an inscribed circle.  Answers are all different but easily calculated from the given parameters.

Worksheet	PowerPoint	Supporting Materials
Triangle xy area	Triangle xy area	None

34. L-centre

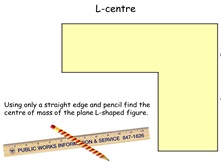
Hands-on activity to find the centre of mass of an L-shaped plane figure by construction only.  But there is something special about them all - each centre of mass is at the inner elbow of the L.  Can the (Year 13) pupils work out why this is?

Worksheet	PowerPoint	Supporting Materials
L-centre	L-centre	L-centre 1 (Geogebra) L-centre 2 (Geogebra)

38. Awkward Triangle

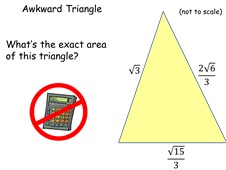
Given the side lengths of a scalene triangle (in surd form) can the pupils work out its area?  Tests use of the Cosine Rule and multiplication and simplification of surds.  For interest, Heron's formula is also used to solve the problem..

Worksheet	PowerPoint	Supporting Materials
Awkward Triangle	Awkward Triangle	Awkward Triangle (Geogebra) Awkward Triangle (Excel)

49. What's the Sine Rule Ratio?

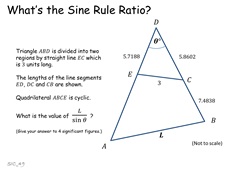
Pupils are asked to use their knowledge of sine rule, cosine rule and even a circle theorem or two to determine angles and lengths in a triangle.

Worksheet	PowerPoint	Supporting Materials
What's the Sine Rule Ratio?	What's the Sine Rule Ratio?	None

Core 1keyboard_arrow_up

Back to Top

5. A Circle Property

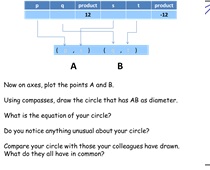
RISP 9.  Pupils choose certain values and draw their own circle.  All circles go through the origin.

Worksheet	PowerPoint	Supporting Materials
A Circle Property	A Circle Property	A Circle Property (Geogebra)

9. Brackets Out, Brackets In

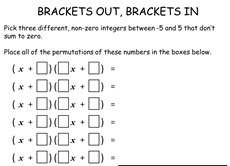
RISP 3.  Pupils have to simplify some algebra, that they have generated.  All have the factor (x+1)

Worksheet	PowerPoint	Supporting Materials
Brackets Out, Brackets In	Brackets Out, Brackets In	Brackets Out, Brackets In (Excel)

19. Cubic Tangent Circle

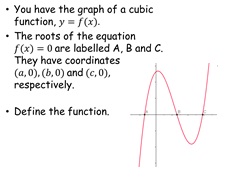
Pupils need to work out the equation of a cubic and draw a tangent at a specific place.  All tangents should go through the first root.

Worksheet	PowerPoint	Supporting Materials
Cubic Tangent Circle	Cubic Tangent Circle	None

20. Hyper Parabola

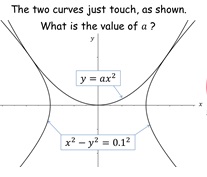
Pupils need to find out where a parabola and a hyperbola just touch.

Worksheet	PowerPoint	Supporting Materials
Hyper Parabola	Hyper Parabola	Hyper Parabola (Geogebra)

28. Survey Plot

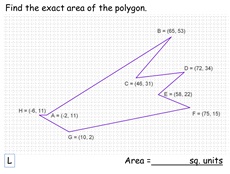
Imagine you needed to remove one metre depth of topsoil from a new building plot.  What volume does this represent?  How many wagons will you need, etc?  By approximating this area to a polygon (where you know the coordinates of the vertices) makes the task very easy (even easier with a spreadsheet).

Worksheet	PowerPoint	Supporting Materials
Survey Plot	Survey Plot	Survey Plot (Excel) Survey Plot (Geogebra)

32. How Close

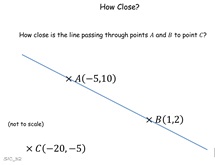
A coordinate geometry task.  Pupils have the coordinates of two points on a line.  How close is this line to a third point?  All pairs of coordinates are different but lie on three different lines - but the closest distance is the same for all.

Worksheet	PowerPoint	Supporting Materials
How Close	How Close	How Close (Geogebra) How Close (Excel)

37. Find f(2)

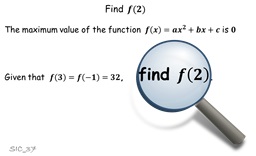
A slightly cryptic question based on a quadratic function.  Not too difficult but a little different from the norm.   As an extension you could ask the pupils to come up with their own parameters that give the same solution.

Worksheet	PowerPoint	Supporting Materials
Find f(2)	Find f(2)	Find f(2) (Geogebra)

Core 2keyboard_arrow_up

Back to Top

13. A Geometric Progression Problem

From clues given about a geometric progression work out the possible solutions - all common ratios are the same and first terms are five times each other.

Worksheet	PowerPoint	Supporting Materials
A Geometric Progression Problem	A Geometric Progression Problem	A Geometric Progress Problem (Excel)

23. A Fractional Sequence

An inductive formula is given with each pupil having different starting values.  They have to find the 11th and 12th terms.  The sequences loop (but they don't know that) so they don't need to go that far.  Then, of course, they have to prove it always loops!

Worksheet	PowerPoint	Supporting Materials
A Fractional Sequence	A Fractional Sequence	A Fractional Sequence (Excel)

24. Area between Parabolas

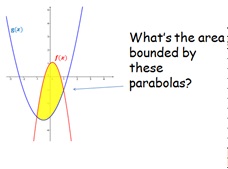
An integration activity around the area bounded by two parabolas.  Some pupils are confused  if the area straddles the x-axis.  This activity addresses this.

Worksheet	PowerPoint	Supporting Materials
Area between Parabolas	Area between Parabolas	Area between Parabolas (Geogebra)

30. Parabola in Parallelogram

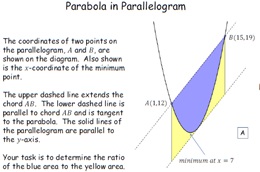
Given certain facts about a parabola the pupils have to determine its equation.  Then they need to integrate the function to work out ratios of areas.  There is a neat solution that makes it very easy to do - which you can show them at the end.  A further extension is to challenge them to do it without integration.

Worksheet	PowerPoint	Supporting Materials
Parabola in Parallelogram	Parabola in Parallelogram	Parabola in Parallelogram (Excel) Parabolas in Parallelogram - no integration (Geogebra)

40. Quadratic Segments

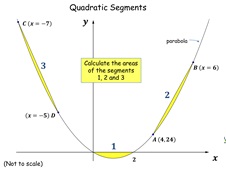
Pupils have to work out the area of three segments formed by chords of equal horizontal widths drawn on a parabola.  Interestingly, this area is invariant for a given width.  They discover this and then hopefully prove it.

Worksheet	PowerPoint	Supporting Materials
Quadratic Segments	Quadratic Segments	Quadratic Segments (Geogebra)

Core 3keyboard_arrow_up

Back to Top

6. Annulus Volume of Revolution

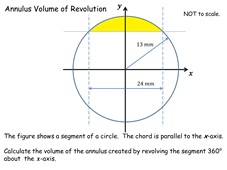
Pupils are given different segments of circles and asked to calculate their volumes of revolution.  They all have the same volume.

Worksheet	PowerPoint	Supporting Materials
Annulus Volume of Revolution	Annulus Volume of Revolution	Annulus Volume of Revolution (Autograph) Annulus Volume of Revolution (Excel) Annulus6 (video) Sunday Times Teaser

14. Integration Stretch

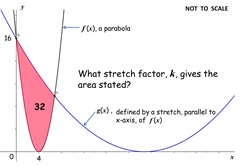
A parabola is stretched - calculate the stretch factor to achieve the area bounded between the two.  All parabolas are different but the stretch factors are the same.

Worksheet	PowerPoint	Supporting Materials
Integration Stretch	Integration Stretch	Integration Stretch (Excel) Integration Stretch (Geogebra)

22. The Shortest Race

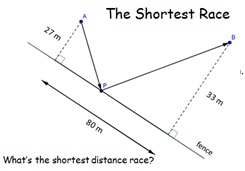
You have to run from tree A to tree B whilst touching a fence.  Where should you touch the fence to minimise the distance you have to run?

Worksheet	PowerPoint	Supporting Materials
The Shortest Race	The Shortest Race	The Shortest Race (Geogebra) The Shortest Race (Excel)

Core 4keyboard_arrow_up

Back to Top

27. Skew Lines

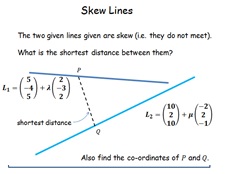
Skew lines in 3D space in vector form.  How close do they get?

Worksheet	PowerPoint	Supporting Materials
Skew Lines	Skew Lines	Skew Lines (Excel) Skew Lines (Autograph)

29. Volume of Tetrahedron

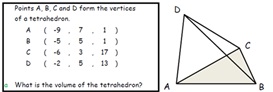
Given the 3D coordinates of four points what is the volume of the tetrahedron that is formed by joining them with line segments?  This brings together just about everything they need to know about vectors and so is a good revision task.  Using the triple product to solve it takes some of the fun out (hence suitable up to C4).  Of course, the volumes are all the same.... but why?

Worksheet	PowerPoint	Supporting Materials
Volume of Tetrahedron	Volume of Tetrahedron Volume of Tetrahedron nets	Volume of Tetrahedron (Excel) Volume of Tetrahedron 1 (Autograph) Volume of Tetrahedron 2 (Autograph) Volume of Tetrahedron net 1 (Geogebra) Volume of Tetrahedron net 2 (Geogebra) Volume of Tetrahedron net 3 (Geogebra) Volume of Tetrahedron net 4 (Geogebra) Volume of Tetrahedron net 5 (Geogebra)

Mechanicskeyboard_arrow_up

Back to Top

26. Shoot the Monkey!

Projectiles.  You want to shoot a monkey hanging in a tree.  But he's a cheeky monkey and at the exact moment you fire, he lets go and falls to the ground.  Knowing this, where should you aim to be sure of hitting your target?

Worksheet	PowerPoint	Supporting Materials
Shoot the Monkey!	Shoot the Monkey!	Shoot the Monkey! (Geogebra) Shoot the Money! (Excel)

33. Target Range

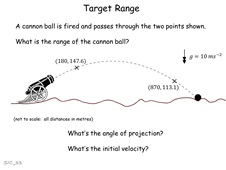
Simple projectiles problem.  Given two points on a trajectory the pupils need to ascertain range, angle of elevation and muzzle velocity.  A good test to see if they can remember how to do it from first principles.

Worksheet	PowerPoint	Supporting Materials
Target Range	Target Range	Target Range (Excel)

34. L-centre

Hands-on activity to find the centre of mass of an L-shaped plane figure by construction only.  But there is something special about them all - each centre of mass is at the inner elbow of the L.  Can the (Year 13) pupils work out why this is?

Worksheet	PowerPoint	Supporting Materials
L-centre	L-centre	L-centre 1 (Geogebra) L-centre 2 (Geogebra)

Statisiticskeyboard_arrow_up

Back to Top

10. Magic Bag

nRich.  An algebra task thinly disguised as a probability question.  The pupils have to determine the number of white balls in a bag.  There are two answers!  Triangular numbers are involved.

Worksheet	PowerPoint	Supporting Materials
Magic Bag	Magic Bag	None

50. Misprints do Hapen

Two proof-readers find errors in the same manuscript - but not all the same ones.  How many are likely to have been missed by both?   This problem seems intractable at first but is quite straightforward if you keep a clear head.  The pupils should be challenged to create a new worksheet with the same answer, 2.

Worksheet	PowerPoint	Supporting Materials
Misprints do Hapen	Misprints do Hapen	None

Further Purekeyboard_arrow_up

Back to Top

44. Sea Shell Product

Pupils discover an intriguing result - the product of the lengths of the chords equals the number of equally spaced dots on the circle.  Quite simple trigonometry and lengths of sides of triangles but the proof is hard!

Worksheet	PowerPoint	Supporting Materials
Sea Shell Product	Sea Shell Product	None