Mr Barton's Rich Tasks

On this page I have collected together my favourite rich tasks that I have used over the last 11 years, in an accessible, easy to use format. I also invite teachers to share their ideas for interesting probing questions and lines of inquiry for students to investigate.
Contents
The Background keyboard_arrow_up
Back to Top
For me, a rich task is one that both engages and challenges students with a wide level of mathematical ability. They need to be “low barrier, high ceiling”, by which I mean students need to have found success/made progress with the task within the first 30 seconds, but there is still enough meat left to keep them thinking 30 minutes (or even 3 lessons) later.
I feel activities like these are crucial for students’ mathematical development. They allow them to be creative, and work together in meaningful and positive ways. When developing our Scheme of Work (you can read my series of blog posts about it), we decided to include a compulsory rich task for all students each topic unit, and many of those can be found below.
The key to a good rich task are the questions that accompany it. This is where effective differentiation happens. All students begin the task in exactly the same way, but once an initial stage has been reached, students (individual or in groups) are free to pursue different investigations, probing questions and lines of inquiry. These can be provided by the teacher, or even by the students themselves.
The strength of the rich task lies in these questions. So here is my plan: I am going to share as many of my favourite rich tasks as possible, and hopefully teachers from around the world are going to provide the questions. These can be lines of inquiry, investigations, prompts, hypotheses, extensions, simplifications, modifications, whatever you like. Crucially, you do not need to know the answer yourself. Just throw it out there! There will be space for these in the Comments section at the bottom of each TES Resource page, and I will always get the ball rolling with a few questions of my own.
Please join in. Please spread the word. Please just share even one question. And then the tasks will keep getting better, and better, and better.
The Rich Tasks keyboard_arrow_up
Back to Top
Task
1 - Positive Differences
Brief Description: Students build simple number pyramids by
taking the positive difference of pairs of numbers
Potential Skills Involved: Arithmetic, Fractions, Decimals,
Writing Expressions, Proof
Task
2 - The Factors and Multiples Game
Brief Description: Students play a strategic game on a
1-100 number grid, crossing off factors and multiples
Potential Skills Involved: Arithmetic, Factors, Multiples,
Primes, Proof
Task
3 - Choose 3 Numbers
Brief Description: Students try to guess each other's
starting numbers by working backwards from the sums of pairs of
numbers
Potential Skills Involved: Arithmetic, Writing expressions,
Solving Equations
Task
4 - Will they meet?
Brief Description: Can you help Romeo and Juliet get back
together in my first ever romantic maths activity?
Potential Skills Involved: Enlargement, Vectors, Similar
Shapes, Rotation
Task
5 - Number Shacks
Brief Description: Can you figure out how the numbers of
these shacks are formed and use this to predict answers and spot
patterns?
Potential Skills Involved: Arithmetic, Writing Expressions
Task
6 - Averaging it out
Brief Description: What happens when we continually take
the mean of sets of numbers?
Potential Skills Involved: Averages, ICT
Task
7 - Fraction Arrangement
Brief Description: Can you order different digits to
produce the biggest and smallest possible answers for these
fraction problems?
Potential Skills Involved: Operations with fractions
Task
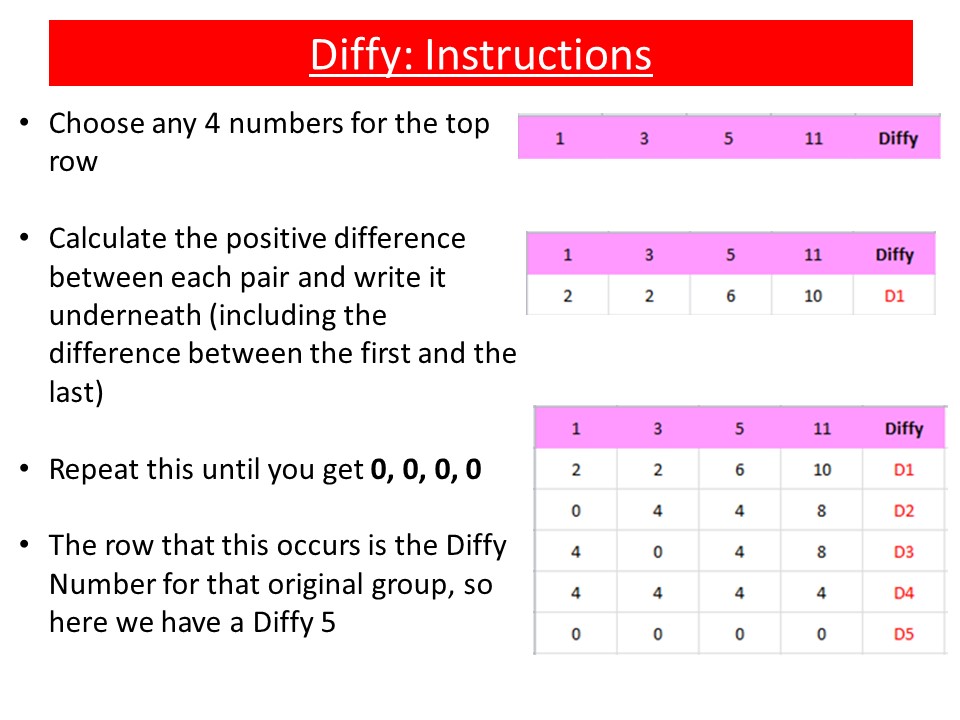
8 - Diffy
Brief Description: The first lesson our new bunch of Year
7s experience, and one of my all time favourites
Potential Skills Involved: Arithmetic, Writing Expressions,
Proof
Task
9 - Simultaneous Equations Staircase
Brief Description: Why does everyone get the same answer to
these simultaneous equation problems?
Potential Skills Involved: Simultaneous Equations, Proof
Task
10 - How many angles?
Brief Description: Using a geoboard, how many angles
between 10 and 180 can you make?
Potential Skills Involved: Angle Facts, Circle Theorems
Task
11 - Number Reverse
Brief Description: What happens when we reverse the digits
of numbers and perform operations on them?
Potential Skills Involved: Arithmetic, Writing expressions,
Proof
Task
12 - Multiplication Reduction
Brief Description: Follow the rule to reduce a number in
size using multiplication. Does anything interesting happen?
Potential Skills Involved: Arithmetic, Writing Expressions
Task
13 - How many quadrilaterals?
Brief Description: Using a geoboard, how many different
quadrilaterals can you make?
Potential Skills Involved: Properties of shapes, Angle
facts
Task
14 - 1089
Brief Description: Why is the number 1089 so special?
Potential Skills Involved: Arithmetic, Writing expressions,
Proof
Task
15 - Square Co-ordinates
Brief Description: What do the co-ordinates of the corners
of squares have in common?
Potential Skills Involved: Co-ordinates, Properties of
shapes, Vectors, Proof
Task
16 - Polar Bears
Brief Description: Can you figure out how to get the totals
in this dice game?
Potential Skills Involved: Arithmetic
Task
17 - Pascal's Triangle
Brief Description: What maths can you discover hiding in
Pascal's triangle?
Potential Skills Involved: Sequences
Task
18 - Entrapment
Brief Description: A fun strategy game using all of the
transformations
Potential Skills Involved: Reflection, Rotation,
Translation, Enlargement
Task
19 - Fire Hydrants
Brief Description: Where is the optimum position to place
these fire hydrants to maximise their coverage?
Potential Skills Involved: Geometrical Reasoning
Task
20 - Diagonals of Rectangles
Brief Description: How many squares does the diagonal of a
rectangle pass through?
Potential Skills Involved: Arithmetic, Sequences, Factors,
Multiples, Primes
Task
21 - T-totals
Brief Description: How can you work out the T-number in
this classic piece of maths coursework?
Potential Skills Involved: Arithmetic, Writing Expressions,
Proof
Task
22 - Number Snakes
Brief Description: What is the longest number snake you can
make using these simple rules?
Potential Skills Involved: Arithmetic, Properties of
Numbers, Writing Expressions
Task
23 - Summing Consecutive Numbers
Brief Description: Which numbers can be made using the sums
of consecutive numbers?
Potential Skills Involved: Arithmetic, Writing Expressions
Task
24 - NIM
Brief Description: The wonderful strategy game using piles
of counters
Potential Skills Involved: Strategy, Factors, Multiples,
Primes
Task
25 - Function Machines
Brief Description: Why do these function machines seem to
give the same difference?
Potential Skills Involved: Arithmetic, Order of Operations,
Writing Expressions, Expanding Brackets
Task
26 - Leap Frog
Brief Description: If you leap over this set of 3 points
enough times, what do you notice?
Potential Skills Involved: Co-ordinates, Construction,
Vectors
Task
27 - Solving Linear Equations
Brief Description: By arranging sets of digits, what types
of solutions can you generate to these simple linear equation
problems?
Potential Skills Involved: Solving linear equations
Task
28 - Decimal Arithmetic
Brief Description: By arranging sets of digits, can you
make the biggest and smallest decimal totals possible?
Potential Skills Involved: Arithmetic, Decimals, Place
Value
Task
29 - 24 Cubes
Brief Description: What different 3D objects can you make
with 24 cubes and what do you notice about their properties?
Potential Skills Involved: Surface Area, Volume, Similarity
Task
30 - Tilted Squares
Brief Description: How many squares with area 1-20 can you
create?
Potential Skills Involved: Area, Pythagoras
Frequently Asked Questions keyboard_arrow_up
Back to Top
Are you saying we should be doing this every lesson?
No. Definitely not. I am acutely aware of the need for students to
gain practise in key mathematical skills. But I do strongly
believe that regular lessons like this are just as important for a
student's mathematical development and to increase their enjoyment
in the subject. They should not be seen as one-offs. Both students
and teachers should value them as highly as any type of lesson.
What do I do if a child doesn't engage with a particular
question or line of inquiry?
The simple answer is that I give them another one! I have to make
a judgment call as to whether the student has genuinely tried and
not just given up too easily. But if, for whatever reason, a
probing question or line of inquiry hasn't resonated with a
student, then I will set them off on something else. Indeed, the
beauty of having lots of questions up your sleeve is that you are
far more likely to find ones that engage your students than if you
just have one line of investigation that the whole class is
following.
Would you do this type of lesson for an observation?
Yes, I definitely would. 100%. Sure, such lessons are a little bit
on the risky side as you don't know what is going to happen. But
they are also incredibly flexible. Imagine you had meticulously
planned a lesson with a 40 slide PowerPoint and 5 beautifully
prepared, differentiated worksheets. And then you find that the
students don't understand even the basics. Or, they understand far
more than you anticipated. You might be in a bit of trouble. But
with a lesson rammed full of probing questions, you can just try
them out on another line of inquiry. Or, better still, get them to
come up with their own.