Talks, Workshops, CPD packages and school support (online and in-person)
For the last 10 years I have been fortunate to deliver keynotes, run workshops, and support maths departments in schools all over the world. My work is always grounded in research, and illuminated with real examples from the classroom. My aim is always the same: to leave teachers with things they can use in their classroom tomorrow, together with strategies and approaches that will last a lifetime. Without wishing to blow my own trumpet, the evaluations and feedback I receive are always outstanding.I am pleased to offer two types of service:
- Tips for Teachers CPD
- Bespoke support and coaching for maths departments
Contents
1. Tips for Teachers CPDkeyboard_arrow_up
Back to Top
Overview
Tips for Teacher CPD is based on the lessons I have learned from interviewing experienced teachers and the world's leading educational experts on my Tips for Teachers podcast, including Dylan Wiliam, Tom Sherrington and Daisy Christodoulou, as well as talented teachers who are not household names.The emphasis is on evidence-based, practical techniques teachers can try in the classroom the very next day.
During the sessions, I present a series of tips. After I have outlined and illustrated each tip, I throw it over to the audience and ask them to consider and discuss with colleagues:
- How does this tip fit into your current practice?
- What would you need to change to make the tip work?
- When could you try the tip for the first time?o they like
the tip?
By the end of the session, teachers have a wealth of tips at their disposal that they can try in the coming days and weeks to improve their teaching. Colleagues will also have access to audio and video recordings of each of the tips to follow up if they want to revisit or dig deeper.
Content
I deliver Tips for Teachers CPD on the following areas (more details in the next section):
- Habits and routines
- The means of participation
- Checking for understanding
- Responsive teaching
- Planning
- Prior knowledge
- Explanations, modelling and worked examples
- Student practice
- Memory and retrieval
- Homework, marking and feedback
The Tips for Teachers CPD is suitable for:
- A keynote at a conference
- A workshop at a conference
- Twilight or inset training
- A half-day CPD session
- A full-day CPD session
- Part of a multi-day CPD package
- Independent, on-demand CPD via my online CPD store
The Tips for Teachers CPD can be delivered:
- Live, in-person
- Live, via a stream (I have a Zoom pro account that can be used at no extra cost)
- Online, on-demand
Content overview
Here are some details about the content of each session.The amount of content I can cover is dependent upon the time allocated for each session.
1. Habits and routines
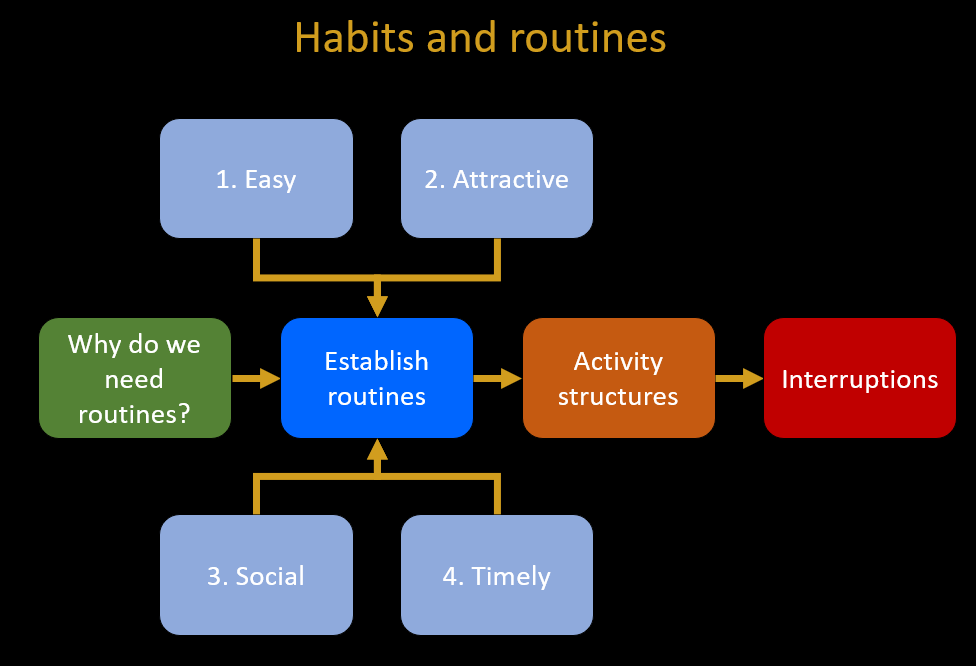
The online, on-demand version of the Habits and Routines workshop is here
2. The means of participation
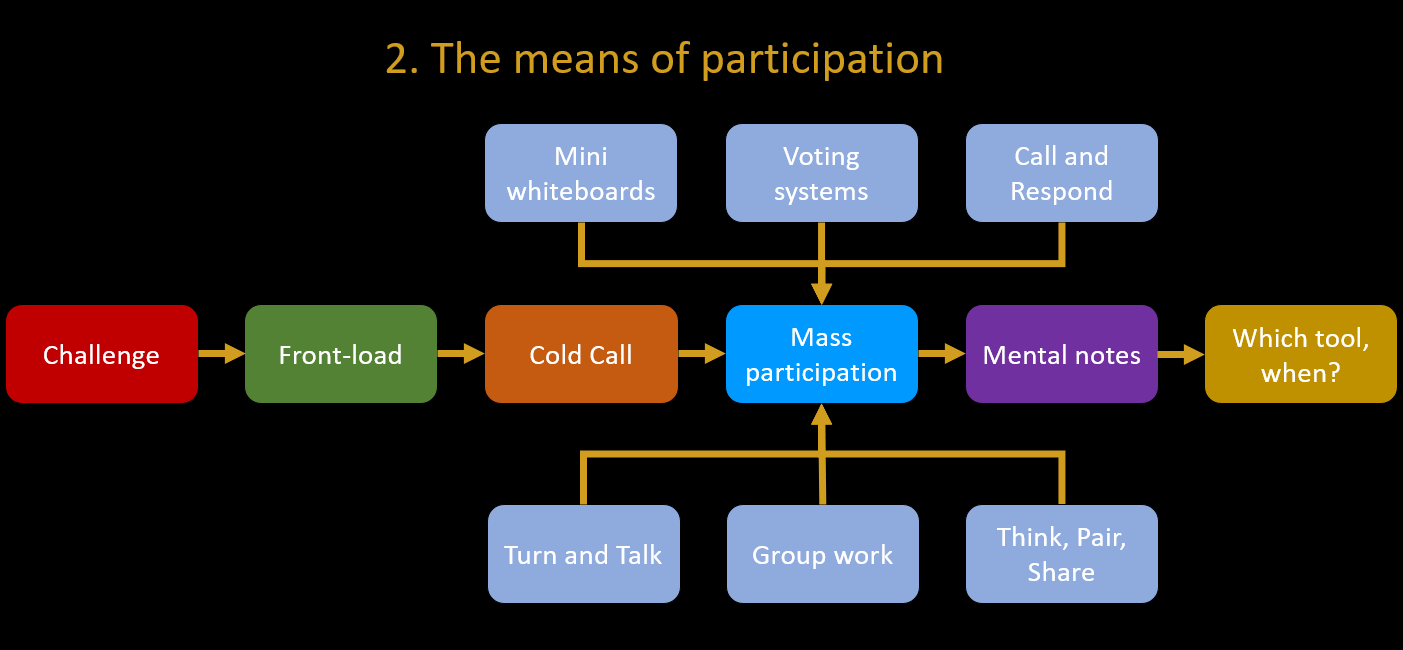
The online, on-demand version of the Means of participation workshop is here
3. Checking for understanding

The online, on-demand version of the Checking for Understanding workshop is here
4. Responsive teaching
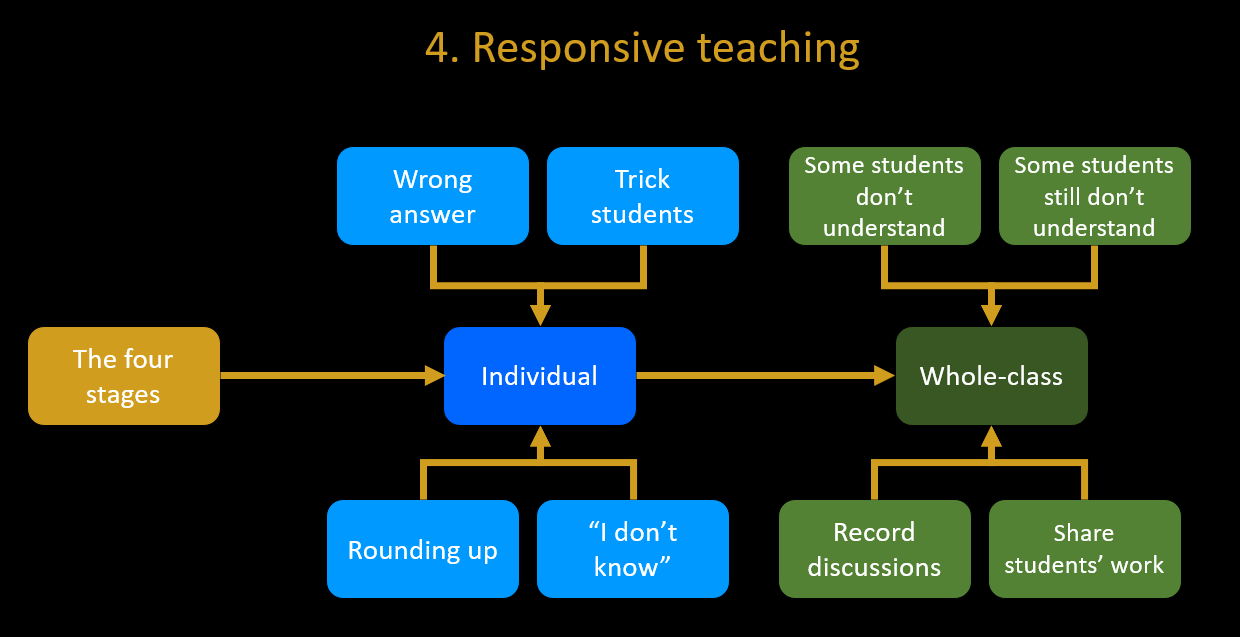
The online, on-demand version of the Responsive teaching workshop is here
5. Planning
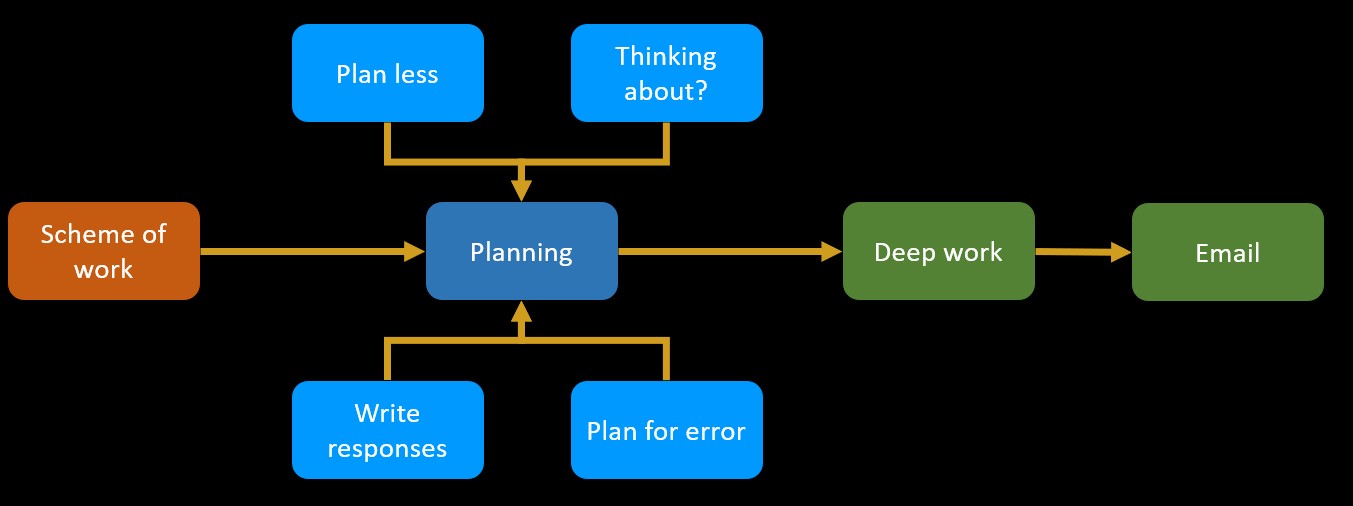
The online, on-demand version of the Planning workshop is here
6. Prior knowledge
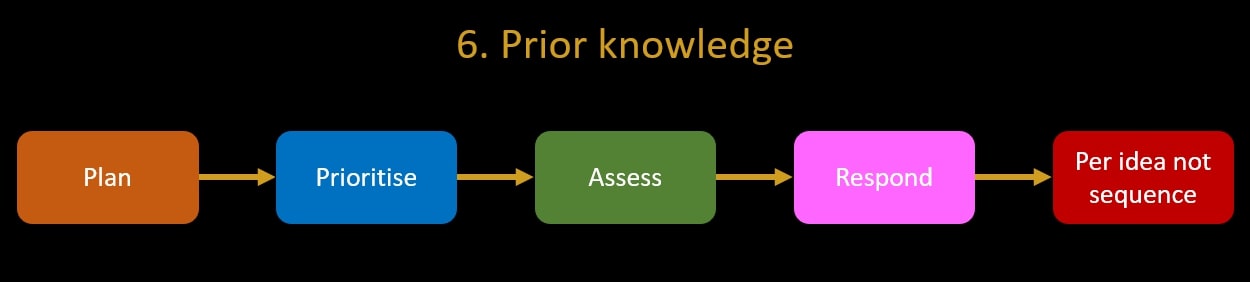
The online, on-demand version of the Prior knowledge workshop is here
7. Explanations, modelling and worked examples
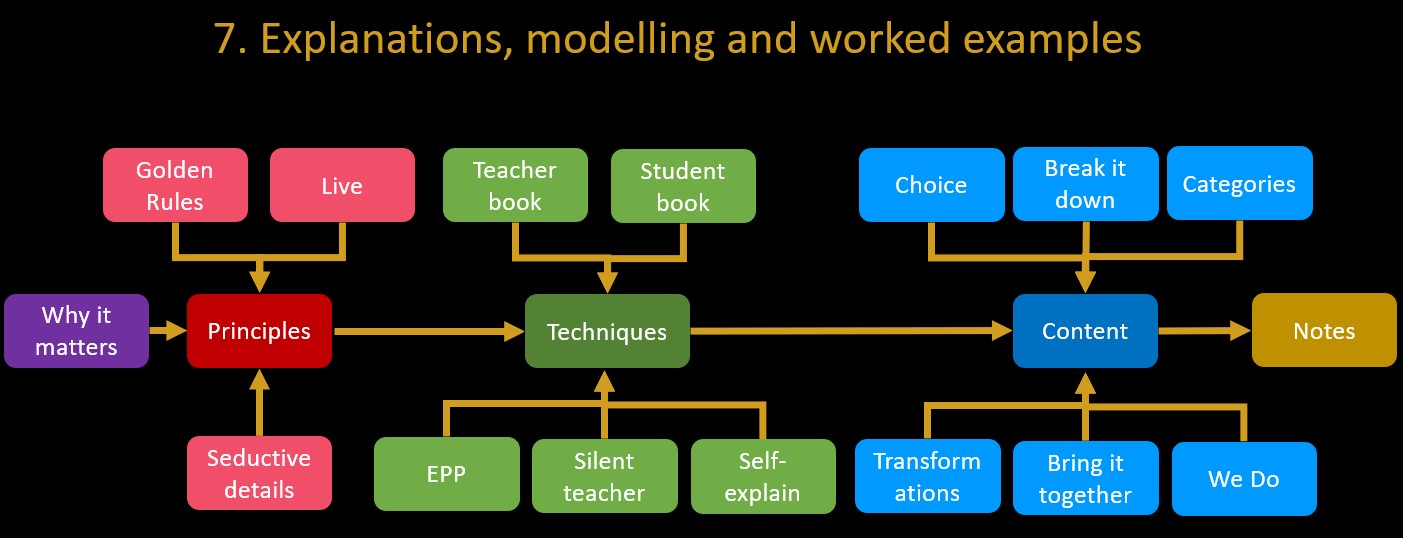
The online, on-demand version of the Explanations, modelling and worked examples workshop is here
8. Student practice
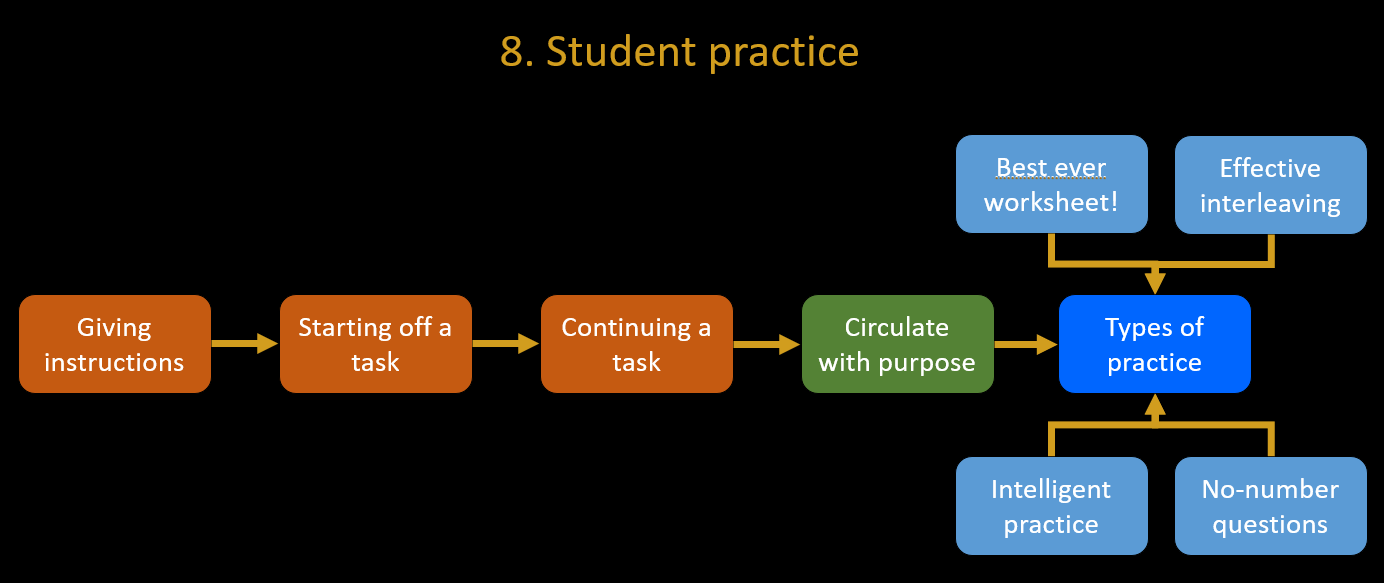
The online, on-demand version of the Student practice workshop is here
9. Memory and retrieval
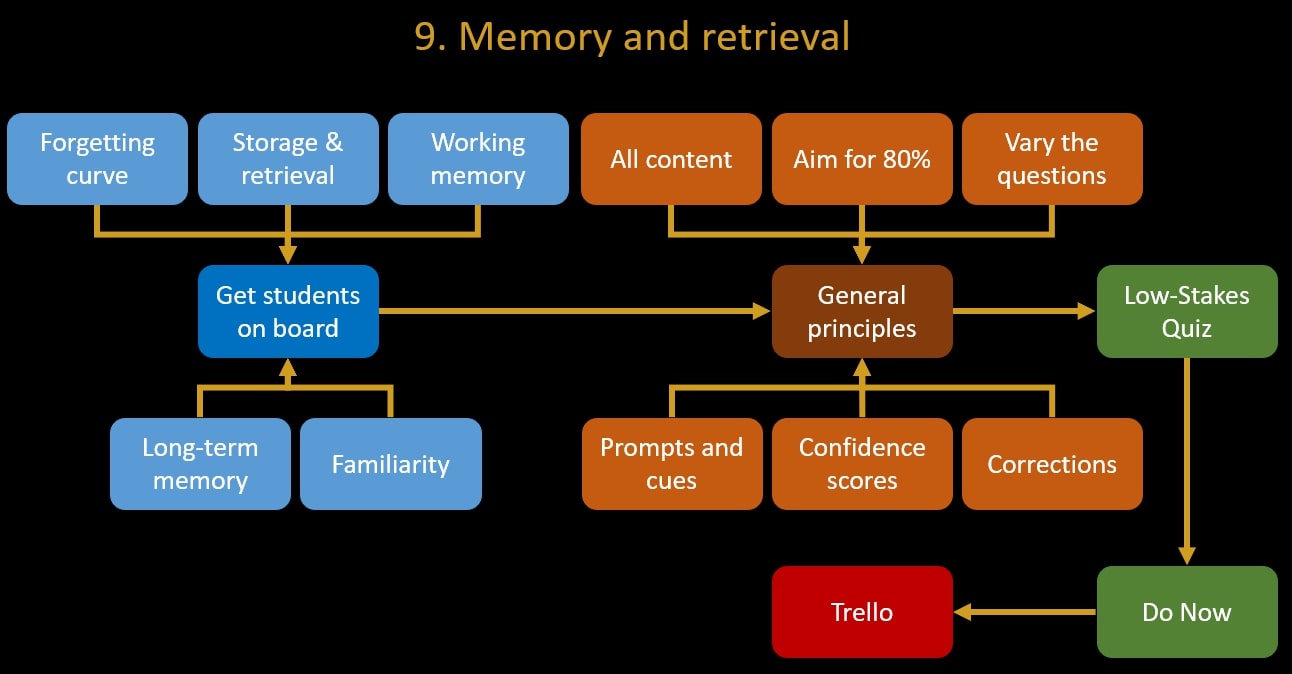
The online, on-demand version of the Memory and retrieval workshop is here
10. Homework, marking and feedback
The online, on-demand version of the Homework, marking and feedback workshop is here
Timings
- A keynote, workshop, or twilight session is best suited to one of these themes.
- A half day’s CPD is best suited to one of these themes
- A full day’s CPD is best suited to two of these themes*
- *Please note: the following workshops can easily cover a full day on their own if you want to go deep!
- 2. The means of participation
- 3. Checking for understanding
- 7. Explanations, modelling and worked examples
- 9. Memory and retrieval
The audience
I have taught maths at secondary school for 15 years, and I only like to talk about things I have tried out myself. So my examples are almost always from the secondary maths classroom.
Over the last 10 years, I have been lucky to deliver whole school sessions and work with primary colleagues, and these sessions have been well received. But I want to be open and honest at the outset - I cannot guarantee all my ideas will transfer to different contexts, and the challenge always lies with the audience to ask themselves: what would I need to change to make this tip work for me, my situation and my students?
A popular model is for me to do a whole-school session in the morning, and then in the afternoon, do something specific with the maths department whilst colleagues from other subjects spend time in their departments reflecting on how they can put the ideas from the morning into practice.
If you want any advice about the likely relevance of certain workshops for different audiences, please mention this when you get in touch.
2. Bespoke support and coaching for maths departmentskeyboard_arrow_up
Back to Top
Back to Top
I have been lucky enough to work closely with many maths departments
across the UK and overseas - both within individual schools and
across Multi Academy Trusts. I offer two types of support, both of which could be one-offs, but work far better if taken as 3 or more days spread out over time:
Maths department support
Here, I work with all the teachers in a department. Through lesson drop-ins, I identify a key area for development, provide bespoke CPD on it, and then the department works together to build it into their practice.A typical visit would work as follows:
- An email exchange with the head of department and/or senior leadership team before the visit to discuss areas of development that have been identified and any important contextual information
- During the morning of the visit, I like to see as many teachers teach as many lessons as possible. The more time in lessons, the better I am able to build up an accurate picture of the support the department needs. I often drop in for no more than a few minutes, before moving on to the next lesson, but then return to a classroom to see how the lesson is progressing
- During my lesson visits, I take notes and photos on my phone as I form hypotheses as to what areas the department could benefit from some support.
- Food! School lunch is ideal – my only dietary fussiness is no fish or mayonnaise!
- A meeting with the head of department (and TLR holders is appropriate) to reflect on the morning and also discuss anything else they may need support with, such as curriculum planning
- 1 hour planning time on my own with wifi access
- An afternoon session with all the department where I highlight the good things I have seen in the morning, and then deliver a bespoke training session based on one of the areas of development I have identified. See the FAQs below for my tech requirements
- If I am lucky enough to return to the school, we can repeat the structure: the morning can be spent looking at how colleagues have implemented the ideas from Day 1, and then in the afternoon we can work on another area of development
Maths coaching
Here I work with individual teachers, 3 or 4 teachers per day. Each teacher chooses a broad teaching goal, I observe the teacher teach, and in the subsequent coaching session, we plan and rehearse steps to get them closer to achieving that goal.Ahead of my visit, please send me the broad teaching goal of each colleague I will be working with. This could be:
- improving a teaching technique across a lesson, such as checking for understanding or modelling
- improving the use of a teaching tool, such as mini-whiteboards or diagnostic questions
- improving a specifc phase of a lesson, such as the Do Now, or when students are practicing independently
- improving lesson planning, such as question and task selection
When planning the day, please try to include:
- A visit to each colleague's lesson in the morning, of between 20 and 40 minutes
- An hour's planning time with access to wifi
- Food! School lunch is ideal – my only dietary fussiness is no fish or mayonnaise!
- An individual coaching session for each colleague of between 30 and 45 minutes in the afternoon
Each coaching session will involve three steps:
- Specific praise
- Hypothesis and critical evidence
- Implementation planning
In subsequent visits, we can take the next logical step to move
closer to the teaching goal.
I always take photos in the lessons I observe to use in the
coaching session. For no extra cost, I can also video some
or all of the lessons I observe. I use an iPhone on a tripod
placed out of the way at the back of the room, and a wireless
lapel mic on the teacher. I can then review the footage with the
coachee in the coaching session, which can be incredibly effective
in helping teachers reflect on their practice and instigate
change. I can send a copy of the footage to the coachee for their
personal records, and the footage will not be used outside of our
coaching session without first seeking permission. If this is
something you are interested in for some or all of your teachers,
let me know and I can bring my recording equipment with me.
I am also happy to use the day to train a coach. A model that
works well here is the trainee coach accompanies me on lesson
visits, we then meet afterwards to discuss our thoughts, and then
plan the coaching session together. This, of course, requires the
consent of the coachee.
For more information about my coaching process, please read the following blog posts. Feel free to share them with staff so they know what to expect!
- An overview of my coaching process
- Coaching case studies #1
- Coaching case studies #2
- Coaching case studies #3
- Coaching case studies #4
The combo!
A popular model is for Day 1 of my support to follow the first model - so I use the morning to identify an area that the department can work on as a team. And then in subsequent visits, we switch to a coaching model so I can work with individual teachers to focus on their specific needs.
If you are interested in booking me for some support, please read the FAQs and Discuss a booking sections below.FAQskeyboard_arrow_up
Back to Top
How long do the full-day CPD events last?
Where possible, I advise factoring in 10 minutes at the start so I can provide an outline of the day, and 15 minutes at the end for reflections, questions and forward-planning. I also suggest at least 45 minutes for lunch - that gives teachers (and me!) time to recharge, ready to make the most of the afternoon session.
Here is an example from a recent event that worked well:
8.45am to 9am: Arrival 9am to 9.10am: Introduction
9.10am to 10.30am: CPD - Part 1
10.30am to 10.45am: Break
10.45am to 12.15pm: CPD - Part 2
12.15pm to 1pm: Lunch
1pm to 2pm: CPD - Part 3
2pm to 2.15pm: Break
2.15pm to 3pm: CPD - Part 4
3pm to 3.15pm: Reflections, questions, forward-planning
I will, of course, do my best to adapt to fit around school lunches, breaks, etc.
How long do the shorter CPD sessions last?
Generally speaking
- A keynote or twilight session: 30 minutes to 90 minutes
- A workshop: 30minution to 2 hours
- A half-day session: up to 3 hours with at least a 15 minute break in the middle
Will you be sharing your slides with the delegates or with
the maths department?
I am afraid I will not be able to share the slides from my CPD sessions, or work with maths departments. This is because:
- I feature many examples (resources, pictures and student work) from the schools I have been lucky enough to work with on my ideas over the last few years, and they have requested that this material is not distributed.
- People pass my slides off as their own - even sell them!
- My slides are often shared out of context on Twitter, leading to many hours of back-and-forths as I try to explain the wider point I am making
- Schools who have booked me in the future have cancelled the event as they have got hold of all my material!
About 90% of what I share in my workshops is freely available on my various websites, and delegates will be directed towards this in the sessions. If delegates wish to take photos of other slides, then so long as they do not share them on social media or with colleagues outside of their school, then that is absolutely fine.
I hope you understand.
What are your requirements in terms of technology/room
set-up/dietary for CPD sessions and work with maths departments?
I can work with most set-ups at in-person events, but the following things are essential:
- Access to a projector / interactive whiteboard
- All delegates can see clearly the writing on the projector/whiteboard - I don't work from hand-outs, so everything will be projected onto the board. This is super-important, as it can really spoil the experience if delegates cannot see properly.
- The ability to connect my own laptop to the projector / interactive whiteboard via HDMI. Please note: I have fonts and software installed on my laptop that mean using a USB on a computer at the venue often leads to problems.
- Access to wifi via my laptop
- If the room is large and needs a microphone, then a radio mic is preferable as I move around a lot! Failing that, a portable mic. The workshops do not work as well if I am rooted to one spot.
- Delegates having access to pens, pencils and paper
- Delegates having tables to write on - i.e. not a lecture theater-style
- A schedule for the day in advance including: start time, end time, lunch, breaks.
And the following things are desirable:
- A mini-whiteboard per person (with pen!)
- Tables arranged in groups of between 4 and 8
- Access to a paper flip-chart / non-interactive whiteboard
- A ready supply of water... tap is fine ;-)
- My only food-related-fussiness is that I don't like fish or mayonnaise!
If any of these are an issue, please let me know in advance and we will try to sort something out.
I don't usually need any of the following:
- Sound
- Printing
If I do need either, I will let you know well in advance.
What are your requirements for on-line events?
I can use your preferred streaming service (Zoom, Microsoft Teams, etc), and if you have the facility to arrange delegates into breakout groups, then we can do our best to replicate the in-person experience in terms of discussion and collaboration. I have access to my own Zoom pro account, and can happily use that to organise the live session with no additional cost to you.
How much does a session cost?
The cost of my in-person training is influenced by travel time. I am based in Leyland, in the North West of England, and hence it is a bit of a trek to most places down south.
The cost will be comprised of a fee (+ VAT), plus travel, accommodation and food where appropriate. For most educational institutions and companies, the VAT can be reclaimed.
I will happy sort out my own transport (economy class train travel and taxis where needed) and accommodation (usually Premier Inn with Meal Deal) and claim it back via the invoice.
The cost of a live-stream will be influenced by the duration and the number of people attending.
I have no limit on the number of people who can attend one of my events. Often schools choose to host an event and then invite colleagues from local schools to help spread the cost. However, if you do intend on charging delegates from other schools to attend, please let me know how much, as I have had some bad experiences with this in the past!
Discuss a bookingkeyboard_arrow_up
Back to Top
Back to Top
If you want to discuss a potential booking, please ensure you have
read through the information above and then drop me an email at mrbartonmaths@gmail.com,
providing as much of the following information as you know:For Tips for Teachers CPD:
- The date of the event (please suggest multiple dates if possible)
- The location of the event if live, or which online platform you are using (you can use my Zoom Pro account for no extra cost)
- The timings of the session
- Your choice of workshop(s) from the list of 10 above
- Relevant information about the audience - subject and phase
- The number of delegates attending
- How much the delegates will be charged to attend
For Maths departmental support and coaching:
- The location of your school
- Some context about the department
- The type of support you are after – departmental, coaching, or a combination of the two
- How many days of support you would like
- A selection of dates that work for you – if considering multiple days of support, I recommend the first two days be as close together as possible
Thanks so much for your interest.
Biography and Photokeyboard_arrow_up
Back to Top
Back to Top
I often get asked to provide a biography and a photo to help promote
the workshops I am involved in. Please find them below.Bio
Craig Barton loves teaching, doing, speaking and thinking about mathematics. He taught maths in secondary schools for 15 years, and was TES Maths Adviser for 10 years. He is now the Head of Education at Eedi. Craig is the author of three best-selling books: “How I wish I’d taught maths”, "Reflect, Expect, Check, Explain" and "Tips for Teachers", the host of the Mr Barton Maths podcast and the Tips for Teachers podcast, and the creator of far too many websites, including mrbartonmaths.com, diagnosticquestions.com, variationtheory.com, ssddproblems.com, dqaday.com and mathsvenns.com. In 2020 he was appointed as Visiting Fellow at the Mathematics Education Centre at the University of Loughborough. Craig has been lucky enough to teach maths and work with teachers and students all over the world. His two proudest achievements are convincing Kate to marry him (and stay married), and being the father to our wonderful boys, Isaac and Jacob.

If you need a high-quality image, then you can download one here.